This is intended to provide a step by step process for summarizing the process.
Sudoku is an easy to learn logic-based number placement puzzle. A Sudoku puzzle consists of 81 cells which are divided into nine columns, rows and regions. The task is now to place the numbers from 1 to 9 into the empty cells in such a way that in every row, column and 3×3 region each number appears only once. A solvable Sudoku must have at least 17 given numbers(1), but normally there are 22 to 30.(1)
To the Left, Image 1 shows a sample Sudoku puzzle. To solve such a puzzle, several techniques can be utilized to solve puzzles. The following is a brief synopsis of these techniques.
Pencilling is a process of tracking what values are possible in each cell. The image below shows a puzzle with all the pencilled values shown. Each cell is split into nine parts, one for each possible number. A known values, like the 5 in the upper left corner allows the user to remove five from all the segments in the first column, first row and the upper left box. This elimination process can be repeated after the value of each cell is determined.
Image 2: Pencilled Puzzle
Single Elimination is the most basic of the Sudoku solution techniques, and was described in pencilling process. Loosely defined, it is the step of assigning the value for a cells once all other numerical possibilities have been eliminated. The image below shows a grey 5 highlighted in the center cell. All other possibilities have been eliminated; ergo that cell's value can be set to will be set to 5. With the center cell set to 5, two other cells, both to the left, can have the fives crossed out. The lower box leaves only one possible value, 9, also highlighted in grey. Progressing this process, the 9 may be eliminated two cells above and that cell can be set at 7. This process can be repeated to solve a good portion of this puzzle, but will not be continued becasue other solution techniques need explanation.
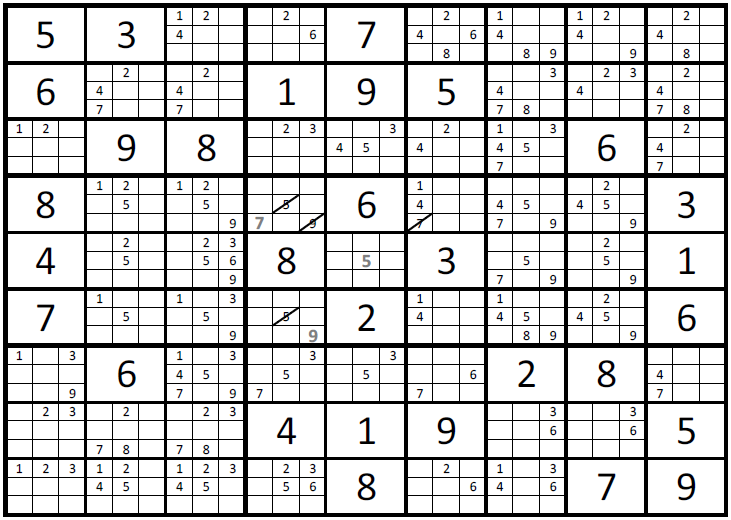Image 3: Single Elimination
Hidden Singles is a process of finding a cell with only option for a given value. The image below shows 3 hidden values highlighted in the blue and pink areas. In the blue area, only one cell in the set can have the number 9; ergo that cell must be a 9. In the pink area, only one cell contains a 7, and another is the only with a 1. Adding this to a solution technique will allow the solution of most Moderate Sudoku puzzles.
Image 4: Hidden Singles
Doubles is an art of eliminating possibilities based on the limiting factors of other cells. If two cells both have the same two possible solutions, then no other cells associated with the set can have those two values as a possibility. No other cell in the same box, row or column as both of the double pair can have the values in the double pair. Image 5 below has an example of a double elimination process. Two cells highlighted in blue are a double pair or with values of 3 and 6. No other cells which in the same box and row, highlighted in blue, can have a 3 or 6 as their solution.
Image 5: Double Elimination
Triple Elimination is similar to Double Elimination, but using three cells. It is key to solving the most Evil puzzles. Image 6 shows an example of a triple Elimination.
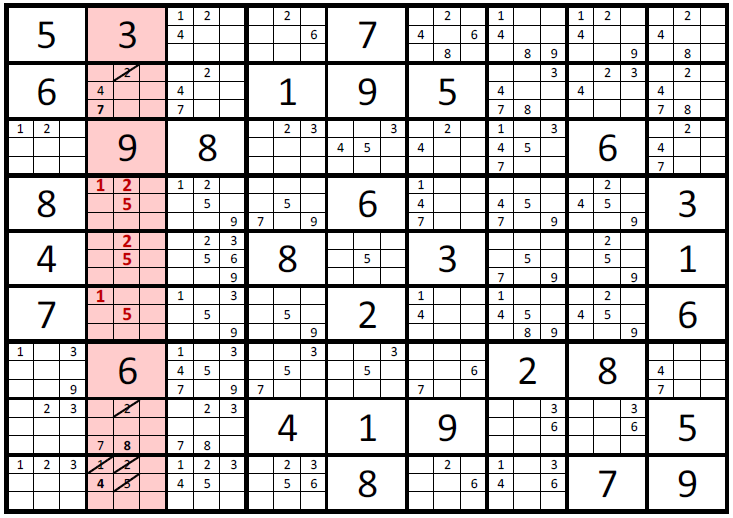Image 6: Triple Elimination
Since Sudoku is a logic-based and not a math-based puzzle, it is possible to make an automated solution system based on conditional statements.
The first decision is to determine the data structures to be used in the solution. The puzzle is a 9 X 9 grid system, which can be numbered as seen in the image below. The cell labels shown will be used to identify cell relationships in the solution.
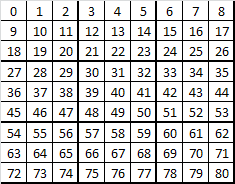Image 7: Puzzle Map
The map puzzle will be stored in a two-dimensional array following the format shown below. The first dimension runs from 0 to 80, or one for each cell in puzzle. The second dimension is a representation of what values are available. The first column represents the number in the cell, if assigned. If the first column is a 0, then a solution for that cell has not been determined. The next nine columns describe what numerals are still available for a cell. A 0 means that numeral is not longer an option, while a 1 indicates that the numeral is an option. If the value is known for a cell, then all the options are zeroed out. The last column is the sum of options. This ensures that if all but one numeral is eliminated, the value can be set quickly simply be looking for these 1 values.
Image 8: Data Array
As noted earlier, cell relationships must be monitored. The next table shows a portion of a map which lists the number of every cell affected by a cell. When a reference cell value is set, then every cell listed in the reference cell's row must be modified based on the reference cell's value.
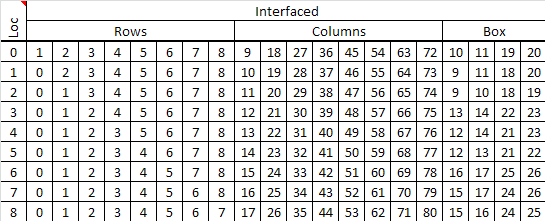Image 9: Cell References
Some additional reference sets are required to handle doubles and triples, but these will not be addressed here.
The following is a summary of the VBA scripts used to obtain a solution to the Sudoku Puzzle. All the subroutines referenced in the spreadsheet are available in the linked excel file. I am assuming that the reader has familiarity with VBA code, and if not, I recommend Mr. Excel's Power Programming with VBA. Previous versions of this book is how I picked up VBA. If you have had exposire to programming, picking up the syntax of another programming language is pretty easy. The first action performed below is to establish the variable arrays that will be used to solve the puzzle.
Option Explicit
'Puzzle Storage
' Puz(i , j) = [Value,1,2,3,4,5,6,7,8,9,Count]
' Value: Value of specific Cell
' 1 - 9: 0 or 1 for if the number is a possible value in the cell
' Count: Number of Possible Values in a Cell. Zero if the Cell Value is determined.
Dim Puz(80, 10) As Integer
'Puzzle Lookup Set 1
' LKP1( i, j) - Input Cell# as i and get interfaced cells with j values.
Dim LKP1(80, 20) As Integer
'Puzzle Lookup Set 2
' LKP2( i, j)
' i sorts groups: Boxes 1-9, Rows 1-9, Cols 1-9
' j sorts 9 tied cells
Dim LKP2(26, 8) As Integer
'Solver Script
Sub Solver()
Dim Done As Boolean 'Variable used to set if Puzzle is completed.
Dim Chk(8) As Integer, Chk2(5, 8) As Integer, Chk3(1, 8) 'Comparison Tools
Dim i As Integer, j As Integer, k As Integer, m As Integer, n As Integer, o As Integer 'Loop Counters
Dim Val As Integer
'Report Start Time
Sheet1.Range("A12") = Time
'Clear End Time
Sheet1.Range("A14") = ""
'Initialize Loop and Completion Variables
Done = False 'Not Complete
'Report Loop and Cycle Values
Sheet1.Range("N11") = 0
Sheet1.Range("R11") = 0
'Reset all Variable for Sudoku Solution
Call ResetData
'Get Inputs from User Input Area
Call GetInputs
'Report All inputs and settings
Call ReportOuputs
'Solution Counter and Cycle Counter
i = 0
o = 0
'Begin Loop through Solution Process
Do While Done = False
'Cycle 1 - Single Possible Value Candidates
For k = 0 To 80
If Puz(k, 10) = 0 Then
i = i + 1
ElseIf Puz(k, 10) = 1 Then
Call DataCheck(k)
Call DataShuffle(k, Puz(k, 0))
i = i + 1
End If
If k = 80 Then
For m = 0 To 80
If Puz(m, 10) = 1 Then
k = -1
i = 0
Exit For
Else
'Do Nothing; Loop cannot converge further.
End If
Next m
o = o + 1
End If
Next k
Call ReportOuputs 'Report Outputs
Val = i 'Backup i Value
'End the Script if all values are accounted for.
Sheet1.Range("R11") = 1
Sheet1.Range("N11") = o
If i = 81 Then
Sheet1.Range("A14") = Time
Exit Sub
End If
'Cycle 2 - Hidden Singles
'Loop Through Sets
For k = 0 To 26
'Reset the Chk Matrix
For m = 0 To 8
Chk(m) = 0
Next m
'Through Chk Matrix Values 1 - 9
For m = 0 To 8
'Add Possible Values in Chk Matrix
For n = 0 To 8
Chk(m) = Chk(m) + Puz(LKP2(k, n), m + 1)
Next n
Next m
'Check for Remainder Values of 1, which indicates that number can only occur in cell of interest.
For m = 0 To 8
If Chk(m) = 1 Then
For n = 0 To 8 'Loop to determine which value has the 1
If Puz(LKP2(k, n), m + 1) = 1 Then
Puz(LKP2(k, n), 10) = 1 'Set Count to 1
Call DataShuffle(LKP2(k, n), m + 1)
i = i + 1
Exit For
End If
Next n
End If
Next m
If k = 26 Then
Call ReportOuputs 'Report Outputs
o = o + 1
If i <> Val Then GoTo NextIteration
Val = i
End If
Next k
'Update Screen upon Completion of Cycle2
Call ReportOuputs 'Report Outputs
Val = i
'End the Script if all values are accounted for.
If i = 81 Then
Sheet1.Range("A14") = Time
Sheet1.Range("R11") = 2
Sheet1.Range("N11") = o
Exit Sub
Else
Sheet1.Range("R11") = 2
Sheet1.Range("N11") = o
End If
'Cycle 3 - Doubles Not implemented
'Cycle 4 - Triples Not implemented
NextIteration:
Loop
Sheet1.Range("A14") = Time
End Sub
This script sets up the file based on the user specified values.
'Get Puzz Data from Excel Sheet1 Yellow Cells at Left
Sub GetInputs()
'Counters
Dim i As Integer, j As Integer, k As Integer
'Puzzle Database Counter
k = 0
For i = 1 To 9 'Loop through Rows
For j = 1 To 9 'Loop through Columns
If Sheet1.Cells(i, j) <> 0 Then
Call DataShuffle(k, Sheet1.Cells(i, j))
End If
k = k + 1
Next j
Next i
End Sub
Data check is used to set the value for a cell with a count value of 1.
'DataCheck sets the value of a cell with a count value of 1.
Sub DataCheck(grid As Integer)
Dim j As Integer, i As Integer
j = 0
If Puz(grid, 10) = 1 Then
For i = 1 To 9
If Puz(grid, i) = 1 Then
j = i
End If
Next i
Else
'Do Nothing
End If
Puz(grid, 0) = j
End Sub
Data shuffle is a process of eliminating possibilities in the puzzle matrix based on the established relationships. So if Cell 3 is assigned a 3, then all the cells related to cell 3 cannot have a 3,and it is eliminated as an option.
'Data Shuffle sets a Puz Cell value Sub DataShuffle(grid As Integer, value As Integer) 'grid - is the number of the Puz cell being set(0-80). 'value is the value to which Puz cell is set(1-9) Dim i As Integer 'Counter 'Set the Puz Cell Value Puz(grid, 0) = value 'Zero out the option values and count For i = 1 To 10 Puz(grid, i) = 0 Next i 'Remove the value option from cells in the shared rows, columns and boxes For i = 1 To 20 If Puz(LKP1(grid, i), value) <> 0 Then 'Only update if needed; Saves processing time Puz(LKP1(grid, i), value) = 0 'Sets option value to 0, ergo value is no longer an option. Call UpdateCount(LKP1(grid, i)) 'Updates the Puz Count for each updated cell. End If Next i End Sub
The following code updates the count column of the puzzle matrix.
'Update Count updates the Column 10 count value in the Puz database for the row indicated by grid Sub UpdateCount(grid As Integer) Dim i As Long 'Counter Dim Temp As Integer 'Counter for Non-Zeros Temp = 0 'Set Placeholder 'Loop Through Columns For i = 1 To 9 Temp = Temp + Puz(grid, i) 'Add Puz options to Temp, only possible values still have a 1 Next i 'Set the Count Value Puz(grid, 10) = Temp End Sub
The following code reports the puzzle in the current solved state to the interface sheet.
'Report Outputs populates the Puz Data to Excel Sheet1 Sub ReportOuputs() 'Counters Dim i As Integer, j As Integer, k As Integer k = 0 For i = 1 To 9 'Loop Through Rows For j = 1 To 9 'Loop through Columns If Puz(k, 0) <> 0 Then 'Only Report Non-Zero Values Sheet1.Cells(i, j + 11) = Puz(k, 0) End If k = k + 1 'Puzz Row Counter Next j Next i End Sub
This last portion of code it to reset all teh variables in the solver, which was necessary when debugging the process. It hangs around to clear out unwanted values in the output table.
'ResetData will reset the spreadsheet, puzzle data and populates the 3 lookup variables
Sub ResetData()
Dim i As Integer, j As Integer 'Counters
Sheet1.Range("L1:T9").ClearContents 'Clear Contents of Sudoku Output Area
'Reset Populate Puz Dataset with a clean slate
For i = 0 To 80
For j = 0 To 10
If j = 0 Then
Puz(i, j) = 0 'All Values to 0
ElseIf j = 10 Then
Puz(i, j) = 9 'All Counts to 9
Else
Puz(i, j) = 1 'All Possibilities to 1
End If
Next j
Next i
'Populate LKP1
For i = 0 To 80
For j = 0 To 20
LKP1(i, j) = Sheet2.Cells(i + 13, j + 1)
Next j
Next i
'Populate LKP2
For i = 0 To 26
For j = 0 To 8
LKP2(i, j) = Sheet2.Cells(i + 2, j + 28)
Next j
Next i
'Populate LKP3
For i = 0 To 80
For j = 0 To 2
LKP3(i, j) = Sheet2.Cells(i + 2, j + 41)
Next j
Next i
'Populate BOX1
For i = 0 To 8
For j = 0 To 5
BOX1(i, j) = Sheet2.Cells(i + 2, j + 46)
Next j
Next i
End Sub
So that is how I built a basic Sudoku Solver. Enjoy!
This lab is dedicated to one of my first programming attempts. The creation of a Soduku Solver.
I have always had a systematic approach to solving a solduku puzzle. Though not the fastest way to solve a puzzle, I have been able to use it to solve even the most difficult Soduku puzzles.
The Solution embarded upon here is based on the following puzzle:
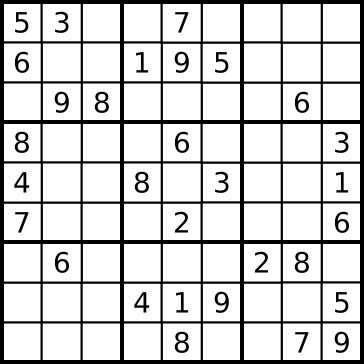Image 1: Sudoku Puzzle
My Program is written the VBA back end of Microsoft Excel. The linked file is a copy of my solver for those who are interested.
SudokuSolver_V1.0.xlsmThis is a basic solver that works for Easy and Intermediate puzzles. The Difficult and Evil puzzles require coding beyond this simple exercise. I do provide descriptions of the tools I use to solve the puzzles. Someday, this process may be converted and embedded in this site.